Einführung
Die spezielle und die allgemeine Relativitätstheorie Einsteins beschreiben Raum und Zeit nicht mehr als getrennte, absolute Größen, sondern sie vereinheitlichen Raum und Zeit zu einer Einheit - der sogenannten Raumzeit. Die spezielle Relativitätstheorie konzentriert sich dabei auf die Relativbewegung zwischen Bezugssystemen nahe der Lichtgeschwindigkeit in der flachen Minkowski Raumzeit. Die allgemeine Relativitätstheorie hingegen beschreibt die Gravitation als eine geometrische Eigenschaft der Raumzeit selbst.
Die aus diesen beiden Theorien resultierenden Konsequenzen entziehen sich unserer Alltagserfahrung. Selbst mit den modernsten Antrieben bewegen wir uns weit unterhalb der Lichtgeschwindigkeit; und die Masse der Erde, möge sie uns auch groß erscheinen, krümmt die Raumzeit gerade so stark, dass wir auf dem Boden bleiben. Die Effekte der allgemeinen Relativitätstheorie treten aber erst deutlich zu Tage, wenn große Massen auf einem kleinen Gebiet komprimiert sind. Das extremste Beispiel ist hier ein schwarzes Loch, wo die Krümmung der Raumzeit so stark wird, dass nicht einmal mehr Licht entweichen kann.
Während die spezielle Relativitätstheorie mathematisch gesehen noch recht einfach ist und auch in der Schule behandelt werden kann, so ist die allgemeine Relativitätstheorie sehr anspruchsvoll. Insbesondere einem Neuling auf diesem Gebiet bereiten die Mathematik wie auch die physikalischen Aussagen beider Theorien große Schwierigkeiten.
Computersimulationen stellen hier einen visuellen Zugang zu beiden Theorien dar. Sie ermöglichen uns, Phänomene wie die Aberration, die Längenkontraktion oder die Lichtablenkung zu 'erfahren'. Damit eröffnen sie uns einen intuitiven Zugang zur speziellen und allgemeinen Relativitätstheorie.
 Beobachter bewegt sich mit 90% Lichtgeschwindigkeit.
Beobachter bewegt sich mit 90% Lichtgeschwindigkeit.
 Blick durch ein Morris-Thorne Wurmloch.
Blick durch ein Morris-Thorne Wurmloch.
Visualisierungstechniken
Die natürlichste Methode für die Visualisierung in der Relativitätstheorie ist die Strahlrückverfolgung (Ray Tracing) vom Beobachter in die Szene. Bei der Erweiterung von drei auf vier Dimensionen ist vor allem die endliche Lichtgeschwindigkeit zu berücksichtigen. Hinzu kommen noch die Frequenzverschiebung des Lichts auf Grund des Doppler-Effekts und gegebenenfalls des Gravitationsfeldes, die Ablenkung der Lichtstrahlen durch die gekrümmte Raumzeit, sowie eventuelle Lichtverstärkungseffekte. Das vier-dimensionale relativistische Ray Tracing liefert qualitativ hochwertige Bilder, es ist jedoch mit sehr hohem Rechenaufwand verbunden und daher für interaktive Visualisierung nicht geeignet.
In der speziellen Relativitätstheorie gibt es mit der bildbasierten Methode und dem Polygon-Rendering zwei prinzipielle Verfahren die interaktive Visualisierung ermöglichen. Beide Verfahren nutzen die moderne Graphikhardware um entweder eine Bild- oder eine Objektraumtransformation durchzuführen. Allerdings gibt es in beiden Fällen gewisse Beschränkungen an die Szene und die Bewegung der Objekte. Eine neu entwickelte dritte Methode kombiniert Polygon-Rendering mit lokalem Ray Tracing und umgeht dabei die Schwächen der beiden zu Grunde liegenden Verfahren.
In der allgemeinen Relativitätstheorie sind interaktive Visualisierungen bisher nur unter Zuhilfenahme analytischer Lösungen für die Bewegungsgleichungen von Licht und Teilchen zu erreichen. Im Fall einer hoch symmetrischen Geometrie der Raumzeit können durch Vorberechnung und Tabellierung einfache Szenen mit interaktiven Bildraten visualisiert werden.
 Visualisierung licht- und zeitartiger Geodäten um Multi-Schwarzloch-Systeme in der Allgemeinen Relativitaetstheorie
Visualisierung licht- und zeitartiger Geodäten um Multi-Schwarzloch-Systeme in der Allgemeinen Relativitaetstheorie
Eine detaillierte Beschreibung findet man hier (nur englisch). (Kommt demnaechst)
 Interactive visualization of a thin disk around a Schwarzschild black hole
Interactive visualization of a thin disk around a Schwarzschild black hole
Eine detaillierte Beschreibung findet man hier (nur englisch).
 GPU-based four-dimensional general-relativistic ray tracing
GPU-based four-dimensional general-relativistic ray tracing
Eine detaillierte Beschreibung findet man hier (nur englisch).
 Detailed study of null and time-like geodesics in the Alcubierre Warp spacetime.
Detailed study of null and time-like geodesics in the Alcubierre Warp spacetime.
Eine detaillierte Beschreibung findet man hier (nur englisch).
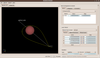 Studying null and time-like geodesics in the classroom.
Studying null and time-like geodesics in the classroom.
Eine detaillierte Beschreibung findet man hier (nur englisch).
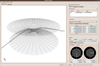 GeodesicViewer - A tool for exploring geodesics in the theory of relativity
GeodesicViewer - A tool for exploring geodesics in the theory of relativity
Eine detaillierte Beschreibung findet man hier (nur englisch).
 Visualizing circular motion around a Schwarzschild black hole
Visualizing circular motion around a Schwarzschild black hole
Eine detaillierte Beschreibung findet man hier (nur englisch).
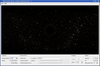 Distortion of the stellar sky by a Schwarzschild black hole
Distortion of the stellar sky by a Schwarzschild black hole
Eine detaillierte Beschreibung findet man hier (nur englisch).
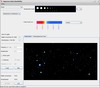 A trip to the end of the universe and the twin "paradox"
A trip to the end of the universe and the twin "paradox"
Eine detaillierte Beschreibung findet man hier (nur englisch).
 Visualization of the General Relativistic Disk of Dust
Visualization of the General Relativistic Disk of Dust
Eine detaillierte Beschreibung findet man hier (nur englisch).
 Visualization in the Einstein Year 2005:
Visualization in the Einstein Year 2005:
A Case Study on Explanatory and Illustrative
Visualization of Relativity and Astrophysics
Eine detaillierte Beschreibung findet man hier (nur englisch).
 Minkowski Diagramme
Minkowski Diagramme
Eine detaillierte Beschreibung der Java2 Applikation findet man hier (nur englisch).
 Relativistic Movement Viewer
Relativistic Movement Viewer
Eine detaillierte Beschreibung findet man hier (nur englisch).
Publikationen
- Müller, Thomas ; Fechtig, Oliver: Empirical exploration of timelike geodesics around a rotating wormhole. In: of Physics, A. J. (Hrsg.) American Journal of Physics, American Journal of Physics. Bd. 84 (2016), Nr. 5, S. 375–383
- Müller, Thomas: Image-based general-relativistic visualization Bd. 36 (2015)
- Müller, Thomas ; Boblest, Sebastian ; Weiskopf, Daniel: Visualization Showcase: General-Relativistic Black Hole Visualization. In: Association, E. (Hrsg.) ; Association, E. (Hrsg.): Eurographics Symposium on Parallel Graphics and Visualization, Eurographics Symposium on Parallel Graphics and Visualization, 2015
- Müller, Thomas: GeoViS – Relativistic ray tracing in four-dimensional spacetimes. In: Computer Physics Communications, Computer Physics Communications. Bd. 185 (2014)
- Müller, Thomas ; Boblest, Sebastian: Visual appearance of wireframe objects in special relativity. In: European Journal of Physics, European Journal of Physics. Bd. 35 (2014)
- Müller, Thomas ; Weiskopf, Daniel: Detailed study of null and timelike geodesics in the Alcubierre warp spacetime. In: General Relativity and Gravitation, General Relativity and Gravitation. Bd. 44 (2012)
- Müller, Thomas ; Frauendiener, Jörg: Interactive visualization of a thin disc around a Schwarzschild black hole. In: European Journal of Physics, European Journal of Physics. Bd. 33 (2012)
- Frutos-Alfaro, Francisco ; Grave, Frank ; Müller, Thomas ; Adis, Daria: Wavefronts and Light Cones for Kerr Spacetimes. In: Journal of Modern Physics, Journal of Modern Physics. Bd. 3 (2012)
- Kuchelmeister, Daniel ; Müller, Thomas ; Ament, Marco ; Wunner, Günter ; Weiskopf, Daniel: GPU-based four-dimensional general-relativistic ray tracing. In: Computer Physics Communications, Computer Physics Communications. Bd. 183 (2012)
- Müller, Thomas ; Boblest, Sebastian: Visualizing circular motion around a Schwarzschild black hole. In: American Journal of Physics, American Journal of Physics. Bd. 79 (2011)
- Müller, Thomas ; Weiskopf, Daniel: General-Relativistic Visualization. In: Computing in Science & Engineering, Computing in Science & Engineering. Bd. 13 (2011), Nr. 6
- Müller, Thomas ; Frauendiener, Jörg: Studying null- and time-like geodesics in the classroom. In: European Journal of Physics, European Journal of Physics. Bd. 32 (2011)
- Boblest, Sebastian ; Müller, Thomas ; Wunner, Günter: Twin paradox in de Sitter spacetime. In: European Journal of Physics, European Journal of Physics. Bd. 32 (2011)
- Müller, Thomas ; Weiskopf, Daniel: Special-Relativistic Visualization. In: Computing in Science & Engineering, Computing in Science & Engineering. Bd. 13 (2011), Nr. 4
- Müller, Thomas ; Grottel, Sebastian ; Weiskopf, Daniel: Special Relativistic Visualization by Local Ray Tracing. In: IEEE Transactions on Visualization and Computer Graphics, IEEE Transactions on Visualization and Computer Graphics. Bd. 16 (2010), Nr. 6
- Müller, Thomas ; Weiskopf, Daniel: Distortion of the stellar sky by a Schwarzschild black hole. In: American Journal of Physics, American Journal of Physics. Bd. 78 (2010), Nr. 2
- Müller, Thomas ; Grave, Frank: GeodesicViewer - A tool for exploring geodesics in the theory of relativity. In: Computer Physics Communications, Computer Physics Communications. Bd. 181 (2010)
- Grave, Frank ; Müller, Thomas ; Dachsbacher, Carsten ; Wunner, Günter: The Gödel Engine - An interactive approach to visualization in general relativity. In: Computer Graphics Forum, Computer Graphics Forum. Bd. 28 (2009), Nr. 3
- Müller, Thomas ; Grave, Frank: Motion4D - A library for lightrays and timelike worldlines in the theory of relativity. In: Computer Physics Communications, Computer Physics Communications. Bd. 180 (2009)
- Grave, Frank ; Buser, Michael ; Müller, Thomas ; Wunner, Günter ; Schleich, Wolfgang P.: The Gödel universe: Exact geometrical optics and analytical investigations on motion. In: Physical Review D, Physical Review D. Bd. 80 (2009)
- Ruder, Hanns ; Weiskopf, Daniel ; Nollert, Hans-Peter ; Müller, Thomas: How Computers Can Help Us in Creating an Intuitive Access to Relativity. In: New Journal of Physics, New Journal of Physics. Bd. 10 (2008)
- Müller, Thomas ; King, Andreas ; Adis, Daria: A trip to the end of the universe and the twin paradox. In: Am. J. Phys, Am. J. Phys. (2008)
- Müller, Thomas: Analytic observation of a star orbiting a Schwarzschild black hole. In: Gen. Rel. Grav., Gen. Rel. Grav. Bd. 41 (2008)
- Müller, Thomas: Falling into a Schwarzschild black hole - Geometric aspects. In: Gen. Rel. Grav., Gen. Rel. Grav. (2008)
- Müller, Thomas: Exact geometric optics in a Morris-Thorne wormhole spacetime. In: Phys. Rev. D, Phys. Rev. D. (2008)
- Müller, Thomas: Einstein rings as a tool for estimating distances and the mass of a Schwarzschild black hole. In: Phys. Rev. D, Phys. Rev. D. Bd. 77 (2008)
- Kobras, D. ; Weiskopf, Daniel ; Ruder, Hanns: General relativistic image-based rendering. In: The Visual Computer, The Visual Computer. Bd. 18 (2002), Nr. 4
- Ruder, Hanns ; Weiskopf, Daniel: Simulation und Visualisierung in der Astrophysik oder die wundersame Reise des Christoph Zenger mit der U.S.S. Enterprise. In: Bungartz, H. J. ; Zimmer, S. (Hrsg.) ; Bungartz, H. J. ; Zimmer, S. (Hrsg.): Numerische Simulation als interdisziplinäre Herausforderung: Beiträge zum 60. Geburtstag von C. Zenger, Numerische Simulation als interdisziplinäre Herausforderung: Beiträge zum 60. Geburtstag von C. Zenger : Springer, 2002
- Kraus, Ute ; Ruder, Hanns ; Weiskopf, Daniel ; Zahn, Corvin: Was Einstein noch nicht sehen konnte. Schnelle Computer visualisieren relativistische Effekte. In: Physik Journal, Physik Journal. (2002), Nr. 7
- Kobras, D. ; Weiskopf, Daniel ; Ruder, Hanns: Image-Based Rendering and General Relativity. In: Proceedings of WSCG’01, Proceedings of WSCG’01, 2001


 DoublePendulum
DoublePendulum