The 12th ACM SIGGRAPH ASIA takes place in Brisbane, Australia on November 17-20, 2019, one of the world's most important conferences in the field of computer graphics and interactive technology. Alongside the conference SIGGRAPH, SIGGRAPH Asia is the second annual meeting of the ACM Special Interest Group on Computer Graphics and Interactive Techniques.
This year VISUS is also represented by the doctoral program Digital Media and the publication "Consistent Shepard Interpolation for SPH-Based Fluid Animation" (authors: Stefan Reinhardt, Tim Krake, Bernhard Eberhardt, Daniel Weiskopf).
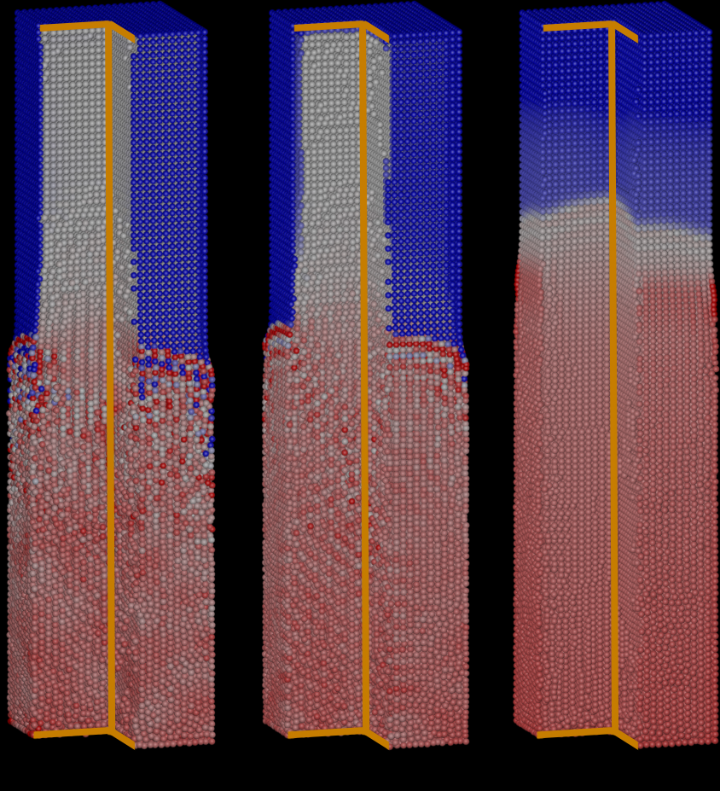
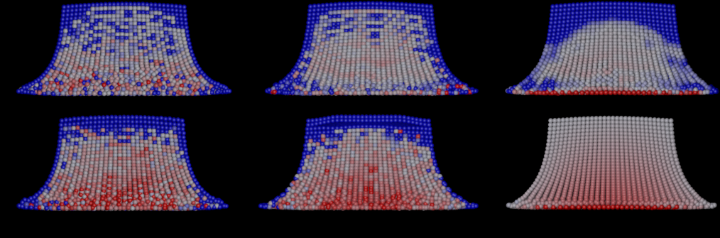
A new technique for correcting discretization errors in Smoothed Particle Hydrodynamics (SPH) based fluid animation is presented. SPH is a Lagrangian technique to simulate fluids and is widely used in the field of computer animation. To simulate the fluid body, the fluid quantities, such as density or pressure, are approximated at given positions. Due to this discretization process, inevitable errors are introduced. The so-called Shepard correction is typically used to reduce this kind of error. This correction scheme, however, employs the density. On the other hand, the density is a fluid quantity itself and undergoes this correction as well. Therefore, the Shepard correction results in an inconsistent scheme.
The authors resolve this issue and present a consistent method to compute the kernel correction. A power method is used to compute the correction factors, resulting in an efficient and unconditionally stable algorithm. In addition, a kernel gradient correction scheme is presented as well as adjustments to a well-known rigid boundary model. The presented method increases the accuracy of the simulation. Moreover, the noise in the density field is significantly reduced, i.e., a smooth density distribution throughout the fluid body is achieved.
Contact

Stefan Reinhardt
M. A.Doctoral Researcher
Patrizia Ambrisi
M.A.Public Relations SFB 1313


